BOJ17779 게리맨더링 2
BOJ 17779 게리맨더링 2
2019년 하반기 삼성전자 역량 테스트 오전 문제이다.
문제를 읽자마자 swea에 있는 SWEA 디저트 카페 문제가 떠올랐다. 5 구역은 마름모 꼴로 형성되기 때문에 가능한 모든 형태의 마름모를 만들고 -> 문제의 선거구 기준에 따라 선거구를 나누고 -> 인구수를 계산하여 문제의 답을 구하는 시뮬레이션 문제이다.
일반적인 사각형 영역이 아닌 마름모 꼴이기 때문에 처음 접하는 사람이라면 어려울 것 같다. 다행히 디저트 카페 문제를 풀어보면서 접한 적이 있었고 비교적 쉽게 풀 수 있었다.
또한, 아래 그림과 같이 5 구역이 마름모 형태가 아니라면 선거구역을 5개로 나눌 수 없다는 것을 인지하고 문제를 풀어야 한다.
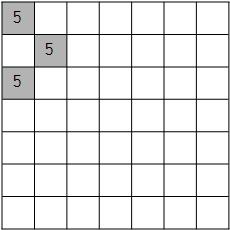
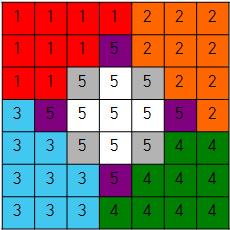
5 구역을 만들고, 1 ~ 4 구역을 나눌 땐 마름모의 꼭짓점을 기준으로 생각한다. 마름모 꼭짓점의 인덱스를 반시계 방향으로 0, 1, 3, 2 이라 생각하고 문제를 해결했다.
1 구역 : 0행 ~ 1번 꼭짓점의 행, 0열 ~ 0번 꼭짓점의 열
2 구역 : 0행 ~ 2번 꼭짓점의 행, 0번 꼭짓점의 열 ~ n-1
3 구역 : n-1 행 ~ 1번 꼭짓점의 행, 0열 ~ 3번 꼭짓점의 열
4 구역 : n-1 행 ~ 2번 꼭짓점의 행, 3번 꼭짓점의 열 ~ n-1
4 개의 구역은 위와 같이 나눠지며 열의 크기를 경계에 맞게 줄이거나 늘리며 설정해준다.
문제 자체는 전형적인 시뮬레이션 구현 문제인데 문제를 이해하는 데 시간이 걸리고 고려해야 하는 조건이 많은 문제 같다.
문제
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.
재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
선거구를 나누는 방법은 다음과 같다.
- 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
- 다음 칸은 경계선이다.
- (x, y), (x+1, y-1), …, (x+d1, y-d1)
- (x, y), (x+1, y+1), …, (x+d2, y+d2)
- (x+d1, y-d1), (x+d1+1, y-d1+1), … (x+d1+d2, y-d1+d2)
- (x+d2, y+d2), (x+d2+1, y+d2-1), …, (x+d2+d1, y+d2-d1)
- 경계선과 경계선의 안에 포함되어있는 5번 선거구이다.
- 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
- 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
- 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
- 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
- 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.
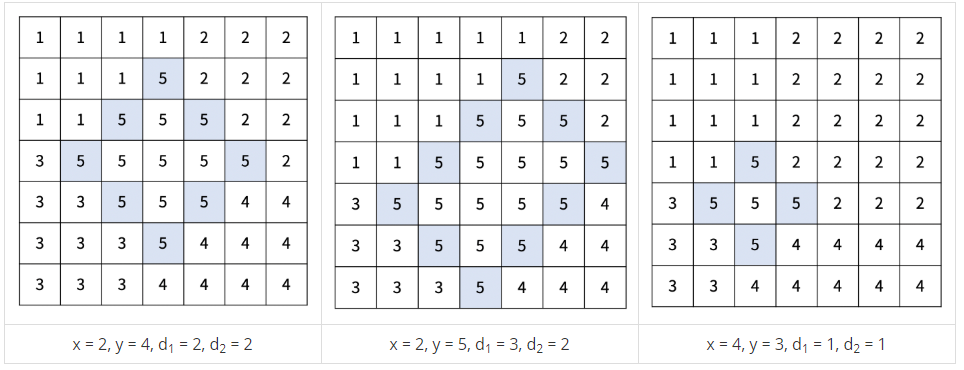
구역 (r, c)의 인구는 A[r][c]이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.
입력
첫째 줄에 재현시의 크기 N이 주어진다.
둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A[r][c]를 의미한다.
출력
첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.
제한
- 5 ≤ N ≤ 20
- 1 ≤ A[r][c] ≤ 100
#include <cstdio>
#include <algorithm>
using namespace std;
struct Point{
int r;
int c;
};
int n;
int city[21][21], area[21][21];
int ans = 987654321;
Point p[4];
bool check(int r, int c, int d1, int d2){
if(r + d1 + d2 >= n || c - d1 < 0 || c + d2 >= n) return false;
return true;
}
void calc(){
int population[5] = {0,};
for(int i=0 ; i<n ; i++){
for(int j=0 ; j<n ; j++){
population[area[i][j]-1] += city[i][j];
}
}
sort(population, population + 5);
ans = min(ans, population[4] - population[0]);
}
void district(){
// 모두 5 구역으로 초기화
for(int i=0 ; i<n ; i++){
for(int j=0 ; j<n ; j++){
area[i][j] = 5;
}
}
int temp = 0;
// 1 구역
for(int i=0 ; i<p[1].r ; i++){
if(i >= p[0].r) temp++;
for(int j=0 ; j<=p[0].c - temp ; j++){
area[i][j] = 1;
}
}
temp = 0;
// 2 구역
for(int i=0 ; i<=p[2].r ; i++){
if(i > p[0].r) temp++;
for(int j=p[0].c+1+temp ; j<n ; j++){
area[i][j] = 2;
}
}
temp = 0;
// 3 구역
for(int i=n-1 ; i>= p[1].r ; i--){
if(i < p[3].r) temp++;
for(int j=0 ; j<p[3].c-temp ; j++){
area[i][j] = 3;
}
}
temp = 0;
// 4 구역
for(int i=n-1 ; i>p[2].r ; i--){
if(i <= p[3].r) temp++;
for(int j=p[3].c+temp ; j<n ; j++){
area[i][j] = 4;
}
}
calc();
}
int main(){
scanf("%d",&n);
for(int i=0 ; i<n ; i++){
for(int j=0 ; j<n ; j++){
scanf("%d",&city[i][j]);
}
}
// 맵 전체를 탐색하여 마름모를 그리고, 꼭짓점을 저장
for(int i=0 ; i<n ; i++){
for(int j=1 ; j<n ; j++){
for(int d1=1 ; d1<=j ; d1++){
for(int d2=1 ; d2<n-j ; d2++){
if(check(i,j,d1,d2)){
p[0].r = i, p[0].c = j;
p[1].r = i + d1, p[1].c = j - d1;
p[2].r = i + d2, p[2].c = j + d2;
p[3].r = i + d1 + d2, p[3].c = j - d1 + d2;
district();
}
}
}
}
}
printf("%d\n",ans);
}
